TURUNAN FUNGSI ALJABAR
A. Definisi
Untuk y adalah fungsi dari x atau y = f(x), turunan fungsi dinotasikan sebagai y' atau f ‘(x) atau dy/dx
Maka turunan fungsi y = f(x) terhadap x didefinisikan sebagai :
Contoh :
Jika f (x) = x2 – 3x, maka turunan fungsi f (x) adalah
B. Rumus Dasar Turunan
- · Turunan fungsi konstan k. Jika f(x) = k, maka f ‘(x) = 0
- · Jika f(x) = ax, maka f ‘(x) = a
- · Jika f(x) = axn, maka f ‘(x) = anxn-1
- · Jika f(x) = u(x) + v(x), maka f ‘(x) = u’(x) + v’(x)
- · Jika f(x) = u(x) . v(x), maka f ‘(x) = u’(x) . v(x) + v’(x) . u(x)
v(x)
maka f ‘(x) = u’(x) . v(x) + v’(x) . u(x)
[v(x)]²
· 7. Jika f(x) = [u(x)]n, maka f ‘(x) = n [u(x)]n-1.u’(x)
· 8. Turunan fungsi komposisi (dalil rantai)
Jika y = f(g(x)), maka = dy = dy .dg
dx dg dx
TURUNAN FUNGSI TRIGONOMETRI
- Jika f(x) = sin x, maka f’(x) = cos x
- Jika f(x) = cos x, maka f’(x) = -sin x
- Jika f(x) = tan x, maka f’(x) = sec2x
PERSAMAAN GARIS SINGGUNG DAN GARIS NORMAL KURVA
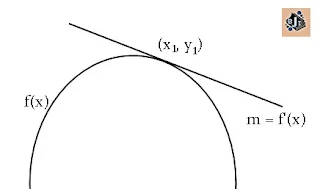
- · Gradien garis singgung kurva di titik (x1,y1) pada kurva f(x) adalah m = f’(x1)
Persamaan garis singgung kurva
y – y1 = m (x – x1)
·
- Garis normal kurva adalah suatu garis yang tegak lurus dengan garis singgung kurva di titik yang sama dengan titik singgung kurva.
· Gradien garis normal kurva di titik (x1,y1) pada kurva f(x)
a adalah mn = -1/f'(x)
· Persamaan garis normal kurva
y – y1 = mn (x – x1)
FUNGSI NAIK, FUNGSI TURUN DAN NILAI STASIONER
- · Fungsi naik
Suatu fungsi dikatakan naik dalam suatu selang untuk x1 < x2 maka f(x1) < f(x2)
kurva naik jika f’(x) > 0
- · Fungsi turun
Suatu fungsi dikatakan turun dalam suatu selang untuk x1 < x2 maka f(x1) > f(x2)
kurva naik jika f’(x) < 0
- · Nilai dan titik stasioner
Jika fungsi f(x) mempunyai turunan pada x = a dan f’(a) = 0, maka f(a) merupakan nilai stasioner fungsi f(x)
Jika f’(a) = 0, maka titik stasioner fungsi adalah (a, f(a))
· Jenis nilai stasioner dimana f”(x) adalah turunan kedua fungsi f(x)
Jika f”(a) < 0, maka f(a) berjenis maksimum
Jika f”(a) > 0, maka f(a) berjenis minimum
Jika f”(a) = 0, maka (a, f(a)) adalah titik belok
CONTOH SOAL DAN PEMBAHASAN
1. Turunan pertama dari fungsi f(x) = 4x3 - 3x2 + 8x -5 adalah….
Pembahasan:
f’(x) = 4.3.x3-1 – 3.2.x2-1+ 8.1 x1-1 -5.0.x0-1
= 12x2 – 6x1 + 8x0 – 0
= 12x2 – 6x + 8
Pembahasan:
misal u(x) = 3x2 +2, u’(x) = 6x
v(x) = 2x -5, v’(x) = 2
maka y’ = u’(x) . v(x) + v’(x) . u(x)
= 6x (2x – 5) + 2 (3x2+2)
= 12x2 – 30 x + 6 x2+ 4
= 18x2 – 30x + 4
3. Turunan pertama dari dari y = (5x2 +3 x)3adalah…
Pembahasan:
misal u(x) = (5x2 +3x), u’(x) = 10x + 3
y = [u(x)]n, maka y' = n [u(x)]n-1.u’(x)
= 3(5x2 +3x)2(10x + 3)
= (30x + 9)(5x2 +3x)2
1. 4. Turunan pertama dari fungsi y = ∛(6x+5) adalah…
y = (6x + 5)1/3, u(x) = 6x = 5, u’(x) = 6
y’ = 1/3 (6x + 5)-2/3(6)
= 2(6x + 5)-2/3
= 2
∛(6x+5)²
5. Turunan pertama dari fungsi f(x) = 3x + 2 adalah…
x - 1
Pembahasan:
u(x) = 3x+2, u’(x) = 3
v(x) = x-1, v’(x) = 1
maka f ‘(x) = u’(x) . v(x) - v’(x) . u(x)
[v(x)]²
= 3(x-1) - 1(3x+2)
(x-1)²
= -5
(x-1)²
6. Persamaan garis singgung para bola y = x2+ 4x -5
pada titik (-1,2) adalah…
Pembahasan:
y’ = 2x + 4
m = 2(-1) + 4 = 2
persamaan garis singgung
y – 2 = 2 (x –(-1))
y – 2 = 2x + 2
y = 2x + 4
2. 7. Persamaan garis normal kurva y = x3-4x2+ 5x-2
pada titik (2,-5) adalah…
Pembahasan:
y’ = 3x2- 8x + 5 = 3(2)2– 8(2) + 5 = 1
mn = -1/y’ = -1/1 = -1
persamaan garis normal
y – (-5) = -1(x-2)
y + 5 = -x + 2
y = -x -7
3. 8. Fungsi f(x) = x2 – 9x naik pada interval…
Pembahasan:
fungsi naik jika f’(x) > 0 ,
maka 2x – 9 > 0
jadi fungsi naik pada x > 4,5
4. 9. Tentukan nilai stasioner dari fungsi f(x) = 2x3 – 15x2 +36x – 10 !
Pembahasan :
titik stasioner dicapai jika f’(x) = 0
6x2 -30x + 36 = 0
6 (x -2) (x-3) = 0
x1 = 2, x2 = 3
Nilai stasioner didapat
f(2) = 18 dan
f(3) = 17
10. Tentukan turunan pertama dari y = sin³(2x+3)
Pembahasan :
y' = 3sin²(2x+3).cos(2x+3) (2)
= 6sin²(2x+3).cos(2x+3)